|
Description
Les « marching squares » désignent un algorithme qui permet de tracer les courbes de niveaux entre les valeurs interpolées d'un champ scalaire en deux dimensions. C'est l'équivalent de l'algorithme des « marching cubes » mais en 2D.
Cet algorithme peut être utilisé par exemple dans la représentation des courbes de niveaux d'altitudes, de températures ou de pressions sur une carte.
Fonctionnement général
Le Marching square :
Cet algorithme fonctionne de la manière suivante, les valeurs sont considérées suivant un maillage, ce qui permet- de traiter les valeurs 4 par 4 , soit un carré dont chaque sommet est caractérisé par son isovaleur.
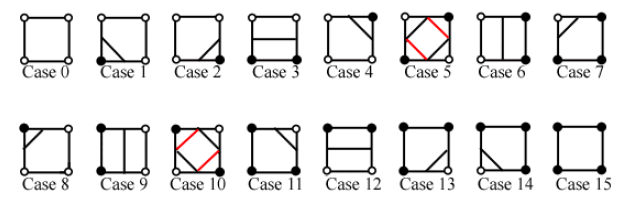
Selon ces isovaleur, et leur supériorité, ou non à l’iso-seuil considéré, chacun des carrés sera représenté par l’un des 16 cas suivants :
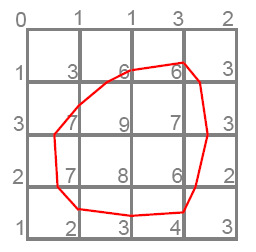
Sur le cas suivant, l'algorithme produirait par exemple :
Travail effectué
Environement de travail : VC++ 6 / librairie Glut (OpenGl)
On fait correspondre les 4 points de chaque cellule à 4 bits. Un bit vaut 1 si le point correspondant est associée à une valeur supérieure à l'isovaleur donnée ou vaut 0 dans le cas contraire. À partir de cela, on obtient un index sur 4 bits de 16 valeurs possibles.
Ces 16 valeurs possibles peuvent être résumées par 4 cas. On a créé une fonction de calcul d'isolignes par cas. On a ensuite associé à chacune de 16 valeurs possibles une des quatre fonctions de calcul d'isolignes.
Les fonctions de calcul d'isolignes effectuent l'approximation d'une l'isoligne par interpolation linéaire entre chaque point.
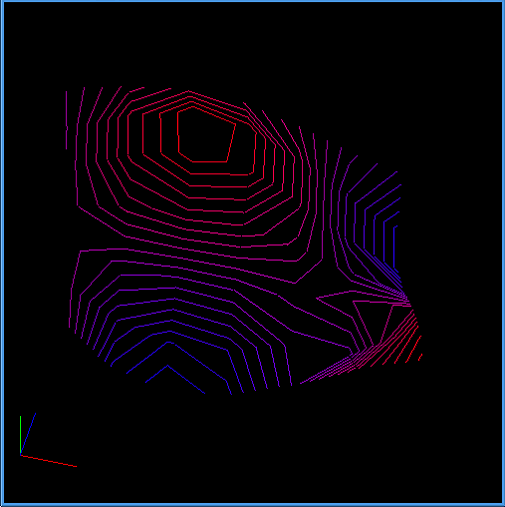
Notre programme trace les isolignes au fur et à mesure de leur calcul. Les isolignes sont colorées en fonction de l'isovaleur à laquelle elles correspondent. Plus l'isovaleur se rapproche de l'isovaleur minimale, plus les isolignes sont bleues, et plus l'isovaleur se rapproche de l'isovaleur maximale, plus les isolignes sont rouges.
Les calculs sont lancés par la fonction void marching_square ().
Ci-dessous, un extrait de notre code source, les fonctions de calcul des quatres cas élementaires :
|
|
|
|
void cas2 (Point2D p1, Point2D p2, Point2D p3, Point2D p4, float v){
Point2D pa, pb;
pa = interpolation (p4, p1, v);
pb = interpolation (p4, p3, v);
glColor3f ((v - fmin) / (fmax - fmin), 0.0, 1.0 - (v - fmin)/(fmax - fmin));
glBegin (GL_LINES);
glVertex3f (pa.x, pa.y, v);
glVertex3f (pb.x, pb.y, v);
glEnd ();
}
void cas3 (Point2D p1, Point2D p2, Point2D p3, Point2D p4, float v) {
Point2D pa, pb;
pa = interpolation (p1, p2, v);
pb = interpolation (p3, p4, v);
glColor3f ((v - fmin) / (fmax - fmin), 0.0, 1.0 - (v - fmin) / (fmax - fmin));
glBegin (GL_LINES);
glVertex3f (pa.x, pa.y, v);
glVertex3f (pb.x, pb.y, v);
glEnd ();
}
void cas4 (Point2D p1, Point2D p2, Point2D p3, Point2D p4, float v) {
Point2D pa, pb, pc, pd;
pa = interpolation (p1, p2, v);
pb = interpolation (p2, p3, v);
pc = interpolation (p3, p4, v);
pd = interpolation (p4, p1, v);
glColor3f ((v - fmin) / (fmax - fmin), 0.0, 1.0 - (v - fmin) / (fmax - fmin));
glBegin (GL_LINES);
glVertex3f (pa.x, pa.y, v);
glVertex3f (pb.x, pb.y, v);
glVertex3f (pc.x, pc.y, v);
glVertex3f (pd.x, pd.y, v);
glEnd ();
} |
|
|
|
|
L'algorithme en action
Cas 1 : Marching square classique
|
|
|
|
void marching_square () {
int nb_niveau = 20;
float niveau;
float pas = (fmax - fmin) / nb_niveau;
int i, j, k;
for (i = 0; i < hauteur - 1; i++) {
for (j = 0; j < largeur - 1; j++) {
for (k = 0; k < nb_niveau; k++) {
niveau = fmin + k * pas;
int bits_iso = 0;
if (P1.v > niveau)
bits_iso |= 8;
if (P2.v > niveau)
bits_iso |= 4;
if (P3.v > niveau)
bits_iso |= 2;
if (P4.v > niveau)
bits_iso |= 1;
switch (bits_iso) {
case 0: break;
case 1: cas2 (P1, P2, P3, P4, niveau); break;
case 2: cas2 (P4, P1, P2, P3, niveau); break;
case 3: cas3 (P2, P3, P4, P1, niveau); break;
case 4: cas2 (P3, P4, P1, P2, niveau); break;
case 5: cas4 (P1, P2, P3, P4, niveau); break;
case 6: cas3 (P1, P2, P3, P4, niveau); break;
case 7: cas2 (P2, P3, P4, P1, niveau); break;
case 8: cas2 (P2, P3, P4, P1, niveau); break;
case 9: cas3 (P1, P2, P3, P4, niveau); break;
case 10: cas4 (P4, P1, P2, P3, niveau); break;
case 11: cas2 (P3, P4, P1, P2, niveau); break;
case 12: cas3 (P2, P3, P4, P1, niveau); break;
case 13: cas2 (P4, P1, P2, P3, niveau); break;
case 14: cas2 (P1, P2, P3, P4, niveau); break;
case 15: break;
}
}
}
}
} |
|
|
|
|
Cas 2 : marching square / parcours par suivi de contours.
Afin d’alléger les traitement, et la représentation de notre isosurface, nous avons tenté une implémentation de suivi de contours. Au lieu d’effectuer un parcours exhaustif de tout le maillage, nous effectuons un parcours sélectif, en suivant les isolignes.

Ainsi ont diminue le nombre de calculs.
Le fonctionnement est récursif : selon de cas de la cellule étudiée, le parcours continu à droite, à gauche, en haut ou en bas, ou dans plusieurs directions. Jusqu'à ce que l’on se trouve sur un bord ou sur une cellule déjà étudiée.
|









