|
Description
Les champs de vecteurs ou de directions sont des objets couramment utilisés pour la visualisation scientifique. Ils associent un vecteur ou une direction à tout point de l’espace, et caractérisent par exemple la vitesse et la direction d’un fluide ou la force et la direction d’une force magnétique ou gravitationnelle correspond à la trajectoire d’une particule sans masse entraînée par le courant.
Si l’écoulement est stationnaire (constant au cours du temps), une particule suit continuellement la même trajectoire, engendrant ainsi la même ligne de courant. Le tracé d’une ligne de courant se fait en général par intégration successive de l’équation de transport du flux par rapport au temps.
Fonctionnement général
Le but de ce TP est de Tracer des streamlines associé à un champ de vecteur.
Le code est écrit en C++ avec les librairies OpenGL.
Nous avons décrit ci-dessus qu’un streamlines est une courbe qui était tangente au vecteur vitesse à un instant t précis. De ce fait, il est indispensable de pouvoir le calculer. Pour mieux comprendre, le fonctionnement, nous verrons d’abord quelques bases mathématiques.

Pour ce TP, notre champ de vecteurs sera associé aux formules mathématiques suivantes :
Vx (x, y, z) = -3 + 6*x - 4*x*(y+1) - 4*z
Vy (x, y, z) = 12*x - 4*x*x - 12*z + 4*z*z
Vz (x, y, z) = 3 + 4*x - 4*x*(y+1) - 6*z + 4*(y+1)*z
Travail effectué
Environement de travail : VC++ 6 / librairie Glut (OpenGl)
Maillage
Nous créeons un maillage 3D à géométrie et topologie régulière, dans l'intervalle [-1;1] pour chaque dimension. Par défaut, le pas du maillage sera réglé sur 6. Nous auront donc 6*6*6 points significatifs dans notre volume.
On affiche le cube qui englobe notre champ dans la fonction afficher_cube ().
On peut également régler le repère en appuyant sur "o", alternant d'une vue orthonormale à une vue en perspective.
Représentation des streamlines
Bases mathématiques
Considérons que le champ vectoriel est un champ de vitesse stationnaire d'un fluide. Si l'on met une particule sans masse dans ce champ, elle va se déplacer selon un vecteur τ(t) dépendant du temps. Pour un intervalle fini t ∈[t0, t1], la particule définie une courbe τ(t), ceci est une streamline.
La forme d'une streamlines τ(t) est déterminée par la direction du champ, en effet la particule se déplace selon un chemin dont le vecteur tangent coïncide avec le champ vectoriel en chaque instant t: d(τ(t))/dt= vitesse
Comme τ est un vecteur en trois dimensions, nous avons un système de trois équations différentielles. Afin de la résoudre, nous devons spécifier la condition initiale τ(t0) = x0, i.e. la position x de la particule au temps t = t0 .
La streamline peut être paramétrée par un autre paramètre que t comme par exemple la longueur de l'arc s. Cela nous sera utile pour parcourir une streamline selon des points équidistants.
Ainsi pour calculer les streamlines, nous avons utilisé plusieurs méthode d’interpolation à savoir :
- Euler
- Modified Euler
- Midpoint
- Rung-Kutta
Interpolation avec la méthode d’Euler
Le problème et de pouvoir calculer les points x(t) à chaque instant sachant que
X(t+Delta_t)= x(t)+Delta_t*Vitesse(x,t)
Vitesse : C’est la vitesse au point x(t)
Delta_t : Intervalle de temps
Cette fonction dérive du développement de Taylor, dans notre cas précis, on s’arrête à l’ordre 1.
Interpolation avec Modified Euler
Le problème est le même la seule différence sera la manière de calculer x(t)
Dans ce cas, nous définissons 2 constantes k qui seront recalculées à chaque point.
K1= Delta_t *Vitesse(x,t)
K2= Delta_t*vitesse(x+k1,t+ Delta_t)
X(t+Delta_t)= x(t)+1/2*(k1+k2)
Interpolation avec Midpoint
Le problème est le même la seule différence sera la manière de calculer x(t)
Dans ce cas, nous définissons 2 constantes k et gmid qui seront recalculées à chaque point.
K1= Delta_t *Vitesse(x,t)
gmid= Delta_t*vitesse(x+k1/2,t+ Delta_t/2)
X(t+Delta_t)= x(t)+Delta_t*gmid
Implémentation
Les différentes méthodes d’interpolation sont disponibles via un menu contextuel accessible par clic droit sur le cube.
Nous avons volontairement choisi d’implémenter uniquement deux de ces méthodes. Deux qui présentent concrétement des différences significatives : Modified Euler et Runge Kutta
|
|
|
|
int euler_stream(float * tail,float * head)
{
float vect[3];
float dt=0.005;
vect[0]=-3 + 6*tail[0] - 4*tail[0]*(tail[1]+1) - 4*tail[2];
vect[1]=12*tail[0] - 4*tail[0]*tail[0] - 12*tail[2] + 4*tail[2]*tail[2];
vect[2]=3 + 4*tail[0] - 4*tail[0]*(tail[1]+1) - 6*tail[2] + 4*(tail[1]+1)*tail[2];
head[0]=tail[0]+(vect[0]*dt);
head[1]=tail[1]+(vect[1]*dt);
head[2]=tail[2]+(vect[2]*dt);
if(fabs(head[0])>1 || fabs(head[1])>1 || fabs(head[2])>1 ||
(fabs(vect[0])<0.01 && fabs(vect[1])<0.01 && fabs(vect[2])<0.01))
{
return 0;
}
return 1;
}
int runge_stream(float * tail,float * head)
{
float dt=0.01;
float vect[3];
float temp[3]={0,0,0};
if(!euler_stream(tail,temp))
return 0;
vect[0]=-3 + 6*tail[0] - 4*tail[0]*(tail[1]+1) - 4*tail[2];
vect[1]=12*tail[0] - 4*tail[0]*tail[0] - 12*tail[2] + 4*tail[2]*tail[2];
vect[2]=3 + 4*tail[0] - 4*tail[0]*(tail[1]+1) - 6*tail[2] + 4*(tail[1]+1)*tail[2];
head[0]=tail[0]+(dt*(vect[0]+temp[0]))/2;
head[1]=tail[1]+(dt*(vect[1]+temp[1]))/2;
head[2]=tail[2]+(dt*(vect[2]+temp[2]))/2;
if(fabs(head[0])>1 || fabs(head[1])>1 || fabs(head[2])>1 ||
(fabs(vect[0])<0.01 && fabs(vect[1])<0.01 && fabs(vect[2])<0.01) )
{
return 0;
}
return 1;
} |
|
|
|
|
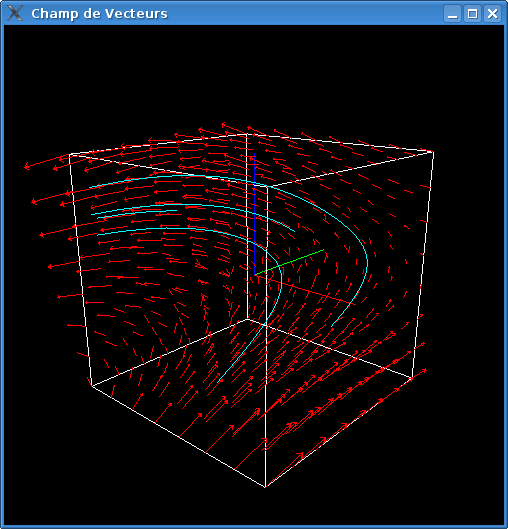
Représentation du champs de vecteurs ainsi que des stream lines
|
|
(perspective)
|
(Projection orthogonale) |
Implémentation de la sonde
Nous voulions donner la possibilité à l’utilisateur de déplacer dans le référenciel une sonde, selon les trois axes. Dans le but de pouvoir analyser l’allure de la stream line en ce point.
Pour cela, nous placons un point au milieu du cube ( sonde verte ).
Cette sonde peut être déplacée avec le bouton central de la souris. Le choix de l’axe selon lequel elle se déplace se fait avec la touche correspondante sur le clavier (X,Y ou Z).
La stream line en ce point est dessinée.
|
|
(perspective)
|
(Projection orthogonale) |
|









